A thorough overview of Bayesian networks, and probabilistic graphical models in general, can be found at the works of Pearl10, Koller and Friedman16, Bishop17, and Nagarajan and Scutari18. Overview of classical univariate and multivariate mixed-effects models can be found e.g. in Mehtätalo and Lappi13. Blei19 describes an iterative procedure of graphical model development and criticism that is followed here. First, a simple model is formulated based on the personal variations that are believed to exist in data. Then, given the data, an approximate posterior is inferenced for the model candidate and it is tested against the data to see if the model is useful or biased. Finally, the model is revised until criteria are met and improvement can be done.
Model specification
Let us denote data with food records and concentration measurements with D and a Bayesian network modeling the data with G. The posterior probability of the network G can be decomposed into a product of data likelihood given the network and a prior probability of that network
$$begin{aligned} P(G|D) propto P(D|G)P(G). end{aligned}$$
(1)
The conditional likelihood of data factorizes further into v independent local distributions of blood concentrations according to their Markov blankets and data are assumed to be grouped by (k = 1,dots ,s) subjects with (n_k) observations for each subject
$$begin{aligned} begin{aligned} P(D|G)&= prod _{i=1}^v P(D|G_i) \&= prod _{d=1}^{n_k} prod _{k=1}^s prod _{i=1}^v P(Y_{ikd} | X_{jkd} = pa_j(Y_{ik})_d, G_i, mu _{ikd}, varvec{phi }_i), j = 1,dots ,p, end{aligned} end{aligned}$$
(2)
where (Y_i) is a random variable for an ith concentration response, and (pa(Y_i)) denotes the set of p observed parent variables for (Y_i) in the directed graph (G_i). Parent variables are direct predecessors of variables in a directed graphical model. Furthermore, (mu _{ikd}) is an expected value of the concentration for a personal observation and set (varvec{phi }_i) pools general parameters of the distribution.
The expected value of the concentration (Y_{ik}) for the subject k is then defined then with a linear predictor that is divided into general and personal parts
$$begin{aligned} begin{aligned} varvec{mu }_{ik}&= varvec{X}_{ik}varvec{beta }_i + varvec{Z}_{ik}varvec{b}_{ik}, \ varvec{X}_{ik}&= pa_X(Y_{ik}), varvec{Z}_{ik} = pa_Z(Y_{ik}) \ {varvec{b}_i}_k&sim mathcal {N}(0, varvec{Sigma }_{b_{ik}}), \ varvec{Sigma }_{b_{ik}}&= varvec{T}_{ik} varvec{C}_{ik} varvec{T}_{ik}’ = varvec{T}_{ik} varvec{L}_{ik} varvec{L}_{ik}’ varvec{T}_{ik}’, \ varvec{T}_{ik}&= diag({sigma _{b_i}^{(1)}},dots ,{sigma _{b_i}^{(p)}}), end{aligned} end{aligned}$$
(3)
where operator (pa_X()) picks the values of observed parent variables from the food record data as a model matrix, and (pa_Z()) picks a similar model matrix for subject k of those food record variables that are assumed to have personal differences between subjects. The model’s assumptions of personal differences are elaborated in the following sections. Furthermore, the variance-covariance matrix ({varvec{Sigma }_b}_{ik}) of personal effects (varvec{b}_{ik}) is defined with a diagonal matrix (varvec{T}_{ik}) containing personal effect standard deviations and personal effect correlation matrix (varvec{C}_{ik}) that decomposes into triangular Cholesky matrix (varvec{L}_{ik}). These matrices are unique to each response variable (Y_i).
The personal effects are calculated as follows by using the estimated matrices (hat{varvec{T}}_{ik}) and (hat{varvec{L}}_{ik}) that describe the effect behaviour
$$begin{aligned} begin{aligned} varvec{z}&sim mathcal {N}(0, varvec{I}) \ hat{varvec{b}}_{ik}&= hat{varvec{T}}_{ik} hat{varvec{L}_{ik}} varvec{z}, end{aligned} end{aligned}$$
(4)
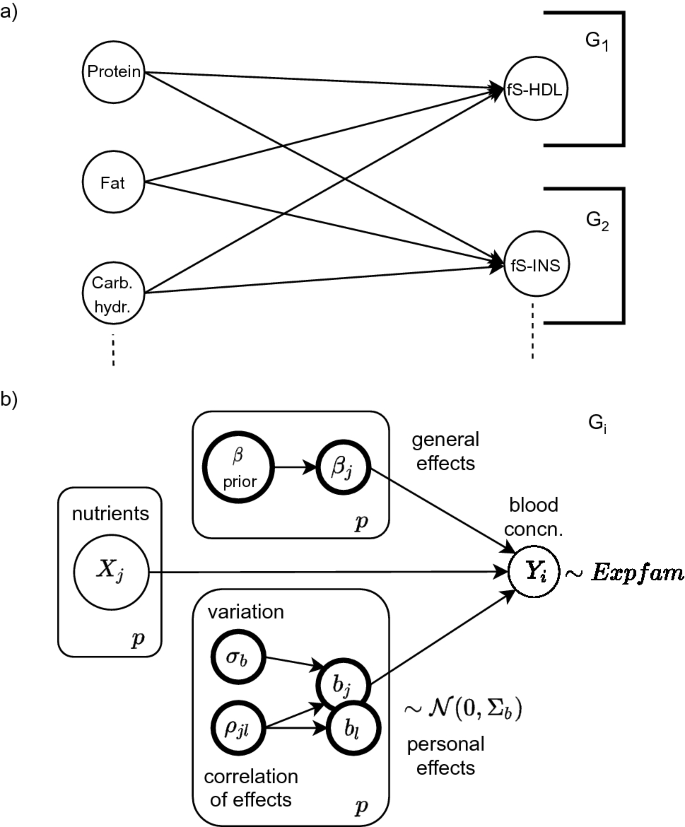
where multiplying standard normal data (varvec{z}) with the learned Cholesky decomposition (hat{varvec{L}}_{ik}) generates a multivariate distribution with the personally correlated effects of nutrients. Then, multiplying it with (hat{varvec{T}}_{ik}) adds the estimated standard deviation of personal effects to the distribution. It should be noted that values in (hat{varvec{b}}_{ik}) are only personal adjustments from the general effects (hat{varvec{beta }}_i) for subject k and the full personal effect is then their sum (hat{varvec{beta }}_i + hat{varvec{b}}_{ik}). The concentration-specific correlation matrix (hat{varvec{C}}_{ik} = hat{varvec{L}}_{ik} hat{varvec{L}}_{ik}’) holds correlations (rho _{jl}) between each (j,l = 1,dots ,p) pair of personal effects (Fig. 2b). This matrix can be further studied for finding the reasoning of personal effect estimates.
In (a) a bipartite Bayesian network is constructed from a few of the variables in Sysdimet data. The overall network factorizes into subnetworks (G_1) and (G_2) that form independently estimated local probability distributions. In (b) a general concentration-specific graphical model (G_i) is shown. It includes p observed random variables X for the nutrient levels and the corresponding concentration level (Y_i). The latent variables of each nutritional effect are estimated from the data. Personal variations ({mathrm {b_i}}) are assumed to follow Normal distribution, but blood concentrations can also be better modeled with Gamma distribution. Evaluation of the directed graphical model starts from the prior and the observed nodes. Their sampled values are propagated as input to downward nodes, and finally, the linear predictor (3) in the concentration node (Y_i) gathers them all and results in an estimation.
Definition of the expected value is further extended to model the correlation of (n_k) successive observations of a person k with a first order auto-regressive process, AR(1),
$$begin{aligned} begin{aligned} y_{ik}^{(t)} = mu _{ik}^{(t)} + rho _i(y_{ik}^{(t-1)}-mu _{ik}^{(t-1)}) + epsilon _t,, t = 2,ldots ,n_k, end{aligned} end{aligned}$$
(5)
where coefficient (rho _i) quantifies the correlation of successive observations of concentration (Y_i), (y_{ik}^{(t-1)}) is a concentration level from the previous personal measurement and (epsilon _t) is noise in the process.
The following sections elaborate considerations on network structure, choices for the personal effect model matrix (varvec{Z}_{ik}), shape of the local distribution P(.), and the prior distribution of general effect parameters (varvec{beta }).
Assumptions for the network structure
Only such networks where nutrients are affecting blood concentrations are considered plausible for modeling the effects of nutrients, and so a network prior (P(G_i) = 1) is set for those networks, and (P(G_i) = 0) for all the others in Eq. (1). This makes all the considered networks bipartite with two layers of random variables. The layers are assumed fully connected and so every nutrient is a possible predictor of any blood concentration. This structure is illustrated in Fig. 2a.
It is also assumed that all the effects from nutrients and other predictors may contain personal differences, and because of that, the inputs are same for both general and personal parts in Eq. (3) by assuming identical model matrices (pa_X(Y_{ik}) = pa_Z(Y_{ik})). It is possible, though, to leave some of the effects common for all the subjects by dropping the corresponding column from (varvec{Z}_{ik}) if it is known that these effects cannot vary among persons.
Distributions of random variables
Normal distribution is used as a starting assumption for all the observed random variables at the network. Reference intakes of nutrients are based on normal distribution20 and so it is practical to use the same distribution for dietary nutrient levels here as well. For the concentration values in Eq. (2) this means (Y_{ik} sim mathcal {N}big (varvec{mu }_{ik}, varvec{Sigma }_{ik}big )) where (varvec{mu }_{ik}) is a vector of expected values from Eq. (3) and (varvec{Sigma }_{ik}) is a covariance matrix of the multivariate distribution.
The blood concentration values are non-negative and usually right-skewed with occasional values greatly above average. This kind of biometric data is usually better modeled with (mathrm {Log-Normal}) or (mathrm {Gamma}) distribution than with normal distribution21. In our model, (mathrm {Gamma}) distribution is considered as an alternative distribution candidate as it allows keeping the regression parameters additive by using an identity link function with (Y_i sim mathrm {Gamma}Big (alpha _i, frac{alpha _i}{g(varvec{mu }_i)}Big )) where (alpha _i) is a shape parameter of (mathrm {Gamma}) distribution and (g(varvec{mu }_i) = varvec{mu }_i) is the identity link function for the expected value. Parameter additivity achieved with the identity link is important as it allows using the same parameter estimates in expected values of both normal and Gamma distributed random variables. This is valuable in future use cases where normally distributed nutrient levels are conditioned from estimated effects and given reference values of concentrations. Parameters are also easier to interpret in the additive scale.
Choices of the prior distribution for the general effects
Parameters of the network are estimated with Bayesian regression. Before the estimation, all predictors are standardized on the same scale. This allows using the parameters (beta _j) and (b_j) at the concentration-specific vectors (varvec{beta }_i) and (varvec{b}_{ik}) in Eq. (3) as direct measures of effect strength. Bayesian modeling allows applying different prior distributions for parameters, and two different prior distributions are considered for the general parameters (beta _j). As a first option, when general effects are studied in detail, it is justifiable to use a vague prior that lets even the weakest of signals to emerge22. Here, Cauchy distribution is used with
$$begin{aligned} begin{aligned} beta _0&sim mathrm {Cauchy(0,10)} \ beta _{j}&sim mathrm {Cauchy(0,2.5)}, j = 1,ldots ,p, end{aligned} end{aligned}$$
(6)
by giving different scales for the intercept and the effect strengths as suggested by Gelman et al.14.
As a second option, when the effects of nutrition are predicted for new subjects, it might be better to use a shrinkage prior that forces weak signals to a minimum and allows the model to generalize better. Piironen and Vehtari23 give a thorough overview of Bayesian shrinkage priors and other model selection methods. For exploring a large number of possible predictors they suggest a projection method, but for this relatively small dataset a regularized horseshoe prior (RHS) is considered suitable. It allows more efficient computation and better predictive performance than the vague prior (6).
Regularized horseshoe prior for general coefficients in (varvec{beta }_i) is defined with
$$begin{aligned} begin{aligned} beta _j&,|,lambda _j, tau , c sim mathcal {N}big (0, tau ^2tilde{lambda ^2_j}big ), \&tilde{lambda ^2_j} = frac{c^2lambda ^2_j}{c^2+tau ^2lambda ^2_j}, \&lambda _jsim mathcal {C^+}(0,1), j=1, ldots ,p, end{aligned} end{aligned}$$
(7)
where (mathcal {C^+}) denotes positive half-Cauchy distribution, (lambda _j) are local scaling parameters for parameters (beta _j), and (tau) is a global scaling parameter. Parameter c here is an additional regularization parameter, and without knowledge of ({beta _j}) parameter scales, a prior distribution suggested by Piironen and Vehtari23 is used, by setting (c^2 sim mathrm {Inv-Gamma}(alpha , beta ),, alpha = nu / 2,, beta = nu s^2 / 2), where (nu) is degrees of freedom. Suggested value for (nu) is 1, but increasing it is reported to help possible computational problems.
Regularized horseshoe prior allows setting a hyperprior for the global shrinkage parameter (tau). This hyperprior (tau _0) allows applying domain knowledge about the number of effective predictors. It regularizes the highest coefficient values and lets the weaker signals to emerge despite the shrinkage. Regularized horseshoe still shrinks some weak signals that the vague prior allows but an optimal value for (tau _0) hyperprior makes it a good compromise for predictions. The value for optimal global shrinkage (tau _0) is calculated from the expected number of nonzero coefficients, (p_0), with
$$begin{aligned} begin{aligned} tau _0 = frac{p_0}{p-p_0}frac{sigma }{sqrt{n}}, end{aligned} end{aligned}$$
(8)
where p is the total number of predictors and (p_0) is in this application the assumed number of nutrients affecting a blood concentration. Piironen and Vehtari22 show further that even a crude guess for number of nonzero parameters improves the prediction accuracy and computation time. With the Sysdimet dataset, it is approximated that one third of the nutrients might be significant for each measured concentration. This makes (tau _0 = frac{7}{22-7}frac{1}{sqrt{424}} approx 0.023).
Sensitivity analysis of the prior choice with the Sysdimet dataset is illustrated in Supplementary Table S4. It shows that estimation of the personal effect standard deviations (hat{sigma }_{bi}) in Eq. (3) is not sensitive to the prior distribution of the general effects (beta _j). The prior choice affects mainly on how the personal effect is shared between the general and personal parts. Regularizing horseshoe prior puts less weight on generally weak effects and gives more weight to personal variations.
Clustering of personal effects
Bayesian network factorizes the joint distribution of concentrations into distinct local distributions. For considering the overall reaction profiles, the personal effects from all the concentrations are pooled together and then clustered for finding self-similar groups of behavior. The clustering is not implemented as part of the model, but in the analysis of the model estimations for gaining more insights on the results. For this, standard k-means clustering24 is applied to the means of personal effect distributions, (hat{varvec{beta }}_i + hat{varvec{b}}_{ik}). It should be noted that in this way the clustering shows only average reactions within the clusters and more extreme personal differences can be found.
In k-means clustering, it is essential to find an optimal number of clusters. The number is approximated with the elbow method25 where a within-cluster sum of squares ratio is plotted for different numbers of clusters. The elbow point of the plot, where this sum of squares ratio stops decreasing substantially, shows the approximate number of clusters that are distinguishing clearly.
Estimation of the Bayesian network
Probabilistic programming language Stan26 was used in implementing and estimating the local probability distributions (G_i) of the Bayesian network as defined in Eq. (2). These blood concentration distributions were estimated with MCMC-sampling by using Stan’s Hamiltonian Monte Carlo (HMC) algorithm and the estimated distributions of parameters were collected as a joint Bayesian network G with a custom R-language code and iGraph27 R-package.
The result is a generative model that allows drawing samples of predicted blood concentrations when a dietary composition is given by using ancestral sampling17. In this method, the root nodes, including fixed hyperpriors of parameters and all the observed inputs, are populated first with values. Their values are then propagated downwards in the directed graph as inputs to the next connected variables until the linear predictors at the concentration variables are reached. Then, all the distribution parameters are estimated and predictions can be drawn. This flow is illustrated in Fig. 2b.
This ancestral sampling is used in posterior predictive checking14,19,28 to evaluate the model fit. The original input data are fed to the graphical model and, if the parameters are estimated correctly, the outcome is expected to match closely the true concentrations. Both visual posterior predictive checks and numerical error metrics are used to detect biased estimations that suggest refining the model structure.